Процедура многокритериального выбора
В методе "ЭЛЕКТРА" разработана процедура многокритериального выбора наиболее предпочтительных объектов, включающая следующие этапы.- Для каждого из критериев вводится дискретная шкала возможных значений этого критерия, весовые коэффициенты критериев.
- Для каждого из критериев строится граф, вершинами которого являются отдельные объекты множества, а дуги указывают на отношение доминирования между объектами в соответствии с данным критерием.
- С учетом важности критериев и предпочтительности объектов вычисляются матрицы значений специальных коэффициентов, называемых индексами согласия и несогласия.
- Для каждой пары объектов (x,y)Є X считается установленным отношение превосходства, скажем х над у, если значение соответствующего индекса согласия больше некоторого порогового значения, а индекс несогласия - меньше соответствующего порогового значения.
- Строится обобщенный граф превосходства, структура которого зависит от выбранных пороговых значений.
Рассмотрим следующую задачу. Пусть Х представляет собой множество абитуриентов, принимающих участие в конкурсных экзаменах при поступлении в технический вуз. На основании проведенных экзаменов необходимо отобрать лучших кандидатов. Состав дисциплин и возможные способы оценки абитуриентов по дисциплинам могут варьироваться согласно специфическим особенностям вуза. Рассмотрим этапы процедуры "ЭЛЕКТРА".
1. В качестве примера рассмотрим оценки трех абитуриентов по трем дисциплинам в пятибалльной шкале.
Таблица - Оценки вступительных экзаменов
| Абитуриенты | Дисциплина | ||
| Математика | Физика | Литература | |
| x | 5 | 3 | 4 |
| y | 5 | 4 | 3 |
| z | 4 | 5 | 3 |
Обозначим:
x,y,z Є X - множество оцениваемых объектов;
xi- оценка объекта Х по критерию i, i = 1..3.
ci - - весовой коэффициент критерия i, i = 1..3, 0 < ci < 1 (10, 100,…)
Пусть c1 = 5, c2 = 3, c3 = 2.
2. Для каждого критерия i строим граф Gi = (X, Vi), где Vi - множество дуг графа Gi. Дуга в графе Giиз вершины х в вершину у существует, если xi ≥ yi. Равенство оценок xi = yi в графе влечет наличие двух дуг из х в у и из у в х.
(x,y) Є Vi ó xi ≥ yi, i = 1..3.
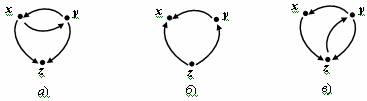
Графы отношений по математике (а), физике (б) и литературе (в)
Построим объединенный граф G0 = (X, V0), где V0 = ∩ Vi есть пересечение трех графов с дугами Vi. Здесь V0 = {Ø}, т.к. в трех графах нет дуг, одновременно совпадающих по направлению. Объединенный граф характеризует полное согласие превосходства одних объектов над другими.

Объединенный граф
3. Строим матрицу индексов согласия превосходства объектов и матрицу индексов несогласия с этим превосходством.
Рассмотрим пару объектов ( x,y)Є X. Применительно к ней множество всех критериев может быть разбито на два "противоположных" класса. К первому классу C(x,y) отнесем все критерии ki, для которых xi ≥ yi, i = 1..3, т.е. критерии, согласно которым в графах Gi имеет место дуга (х, у): C(x,y) = {ki|(x,y) Є Vi, i=1..3|}.
C(x,y) = {k 1, k3}; C(x,z) = {k1, k3}; C(y,x) = {k1, k2}
C(y,z) = {k1, k3}; C(z,x) = {k2}; C(z,y) = {k2,k3},
где k1 -математика, k 2- физика, k3 - литература.
Ко второму классу D(x,y) пары объектов (x,y) отнесем критерии ki, для которых отсутствуют в графах Gi дуги (x,y): D(x,y) = {ki|(x,y) ≠Vi, i=1..3|}.
D(x,y) = {k2}; D(x,z) = {k2}; D(x,y) = {k3};
D(y,z) = {k2}; D(z,x) = {k1, k3}; D(z,y) = {k1}
Рассчитываем матрицу для индексов согласия по формуле:
где ci - весовой коэффициент критерия ki ;
Матрица индексов согласия будет иметь вид:
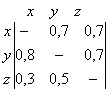
Индексы согласия в матрице c(x,y) могут изменяться от 0 до 1 и выражают степень согласия о предпочтении х над у.
Рассчитываем матрицу для индексов несогласия по формуле:
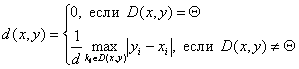
где d - нормирующий коэффициент, равный максимальному разбросу оценок на всем множестве критериев.
Матрица индексов несогласия будет иметь вид:
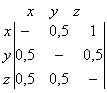
Индексы несогласия d(x,y) в матрице могут изменяться от 0 до 1 и выражают степень несогласия, недоверия к превосходству х над у.
Абсолютная уверенность в превосходстве х над у будет при c (x,y) = 1 и d(x,y) = 0. В объединенном графе G0 в этом случае будет дуга (х,у).
4. Вводится отношение превосходства на объектах через пороговые значения p и q. Значение порога p вводится для индексов согласия и должно быть ближе к единице, значение порога q вводится для индексов несогласия и должно быть ближе к нулю. Говорят, что объект х превосходит объект у, если c(x,y) ≥ p и d(x,y) ≤ q, т.е. выполняются следующие условия:
- совокупность критериев (с учетом их относительной важности), по которым x>y достаточна представительна (порог p);
- оценки по остальным критериям не дают достаточных оснований (порог q) для отказа о превосходстве x>y, степень недоверия к этому предположению не выходит за допустимый предел qi.
5. Обобщенный граф превосходства G0(1;0) при p=1 и q=0 представлен на рисунке. В графе G (p,q) появится дополнительная дуга, например, если верхний порог p=0,8, а нижний порог q = 0,5. Всегда G0(1;0) является частичным графом G(p',q'), если p' < 1, а q' > 0.
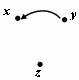
Обобщенный граф G(0,8;0,5)